Определения тригонометрических функций в прямоугольном треугольнике
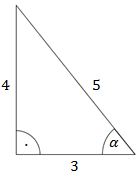
В прямоугольном треугольнике обозначим один острый угол буквой:
стороны и - катеты прямоугольного треугольника.
сторона - гипотенуза прямоугольного треугольника.
С указанными выше обозначениями у нас есть следующие определения тригонометрических функций:
или словами:
Графический метод запоминания
Чтобы вычислить синус острого угла в прямоугольном треугольнике:
- смотрим сначала в сторону, противоположную углу,
- затем к гипотенузе.
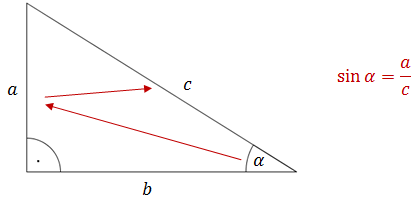
Чтобы вычислить косинус острого угла в прямоугольном треугольнике:
- сначала смотрим на основание прямоугольника,
- затем к гипотенузе.
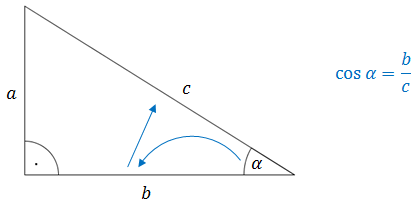
Чтобы вычислить тангенс острого угла прямоугольного треугольника:
- смотрим сначала в сторону, противоположную углу,
- затем к основанию треугольника.
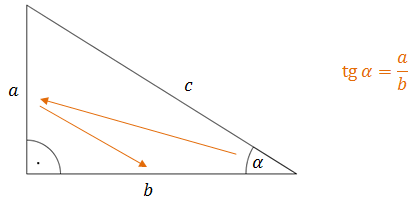
Чтобы вычислить котангенс острого угла в прямоугольном треугольнике:
- сначала смотрим на основание прямоугольника,
- затем в сторону, противоположную углу.
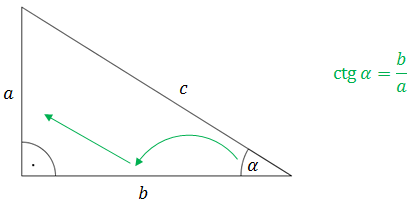
Доказательство тригонометрической формулы для острого угла в прямоугольном треугольнике
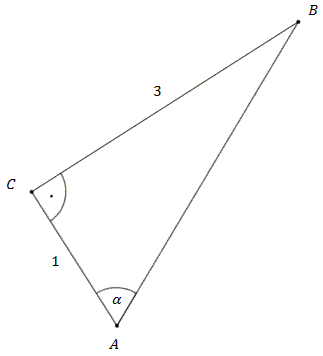
Возьмем любой прямоугольный треугольник и отметим в нем острый угол .
По определению тригонометрических функций мы знаем, что:
Следовательно: Из теоремы Пифагора мы знаем, что: Следовательно:По определению тригонометрических функций мы знаем, что:
Следовательно: и: а также:Когда мы знаем значение хотя бы одной тригонометрической функции, то с помощью приведенные выше формулы мы можем рассчитать значения всех остальных тригонометрических функций.
