Математика
Окно имеет форму прямоугольника, ограниченного сверху полукругом (рисунок \(3\)). Периметр окна равен \(P.\) Определить радиус полукруга \(R,\) при котором площадь окна является наибольшей.
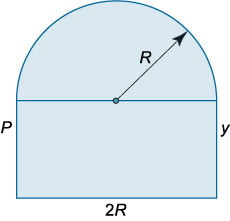
Очевидно, что одна сторона прямоугольника равна \(2R.\) Другую сторону обозначим через \(y.\) Периметр всего окна выражается формулой
\[P = \pi R + 2R + 2y.\]
Отсюда находим \(y:\)
\[y = \dfrac{1}{2}\left[ {P - \left( {\pi + 2} \right)R} \right].\]
Площадь окна составляет:
\[ {S = \dfrac{{\pi {R^2}}}{2} + 2Ry } = {\dfrac{{\pi {R^2}}}{2} + 2R \cdot \dfrac{1}{2}\left[ {P - \left( {\pi + 2} \right)R} \right] } = {\dfrac{{\pi {R^2}}}{2} + PR - \pi {R^2} - 2{R^2} } = {PR - \dfrac{{\pi {R^2}}}{2} - 2{R^2}.} \]
Полученное выражение представляет собой функцию \(S\left( R \right).\) Исследуем ее на экстремум. Находим производную:
\[ {S'\left( R \right) = {\left( {PR - \dfrac{{\pi {R^2}}}{2} - 2{R^2}} \right)^\prime } } = {P - \pi R - 4R } = {P - \left( {\pi + 4} \right)R.} \]
Определяем стационарные точки:
\[ {S'\left( R \right) = 0,}\;\; {\Rightarrow P - \left( {\pi + 4} \right)R = 0,}\;\; {\Rightarrow R = \dfrac{P}{{\pi + 4}}.} \]
Поскольку вторая производная отрицательна:
\[
{S''\left( R \right) = {\left[ {P - \left( {\pi + 4} \right)R} \right]^\prime } }
= { - \left( {\pi + 4} \right) < 0,}
\]
Само максимальное значение площади составляет
\[ {{S_{\max }} = PR - \dfrac{{\pi {R^2}}}{2} - 2{R^2} } = {P\left( {\dfrac{P}{{\pi + 4}}} \right) - \left( {\dfrac{\pi }{2} + 2} \right){\left( {\dfrac{P}{{\pi + 4}}} \right)^2} } = {\dfrac{{{P^2}}}{{\pi + 4}} - \dfrac{{\left( {\cancel{\pi + 4}} \right){P^2}}}{{2{{\left( {\pi + 4} \right)}^{\cancel{2}}}}} } = {\dfrac{{2{P^2} - {P^2}}}{{2\left( {\pi + 4} \right)}} } = {\dfrac{{{P^2}}}{{2\left( {\pi + 4} \right)}}.} \]