Тригонометрия

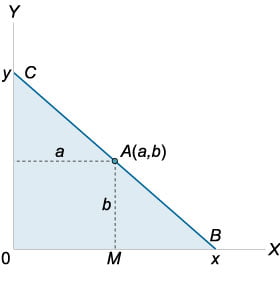
Рассмотрим треугольники \(OBC\) и \(MBA.\) Эти треугольники подобны. Следовательно, справедливо соотношение

\[\dfrac{{OC}}{{MA}} = \dfrac{{OB}}{{MB}}\;\;\text{или}\;\;\dfrac{y}{b} = \dfrac{x}{{x - a}},\]

где координаты \(x\) и \(y\) удовлетворяют соотношениям \(x > a,\) \(y > b.\) Отсюда выразим \(y\) через \(x:\)

\[y = \dfrac{{bx}}{{x - a}}.\]

Площадь треугольника будет описываться следующей функцией \(S\left( x \right):\)

\[ {S\left( x \right) = \dfrac{{xy}}{2} = \dfrac{x}{2} \cdot \dfrac{{bx}}{{x - a}} } = {\dfrac{{b{x^2}}}{{2\left( {x - a} \right)}}.} \]

Вычислим производную:

\[ {S'\left( x \right) = {\left( {\dfrac{{b{x^2}}}{{2\left( {x - a} \right)}}} \right)^\prime } } = {\dfrac{b}{2}{\left( {\dfrac{{{x^2}}}{{x - a}}} \right)^\prime } } = {\dfrac{b}{2} \cdot \dfrac{{2x\left( {x - a} \right) - {x^2}}}{{{{\left( {x - a} \right)}^2}}} } \] \[= {\dfrac{b}{2} \cdot \dfrac{{2{x^2} - 2ax - {x^2}}}{{{{\left( {x - a} \right)}^2}}} } = {\dfrac{{bx\left( {x - 2a} \right)}}{{{{\left( {x - a} \right)}^2}}}.} \]

Функция \(S\left( x \right)\) имеет критические точки \(x = 0,\) \(x = a,\) \(x = 2.\) Поскольку \(x > a,\) то решением является точка \(x = 2a.\) При переходе через нее производная меняет знак с минуса на плюс, т.е. \(x = 2a\) − точка минимума функции \(S\left( x \right).\)

Вычислим другой катет треугольника:

\[\require{cancel} y = \dfrac{{bx}}{{x - a}} = \dfrac{{b \cdot 2a}}{{2a - a}} = \dfrac{{2\cancel{a}b}}{\cancel{a}} = 2b. \]

Таким образом, треугольник с наименьшей площадью имеет катеты, равные \(2a\) и \(2b.\)