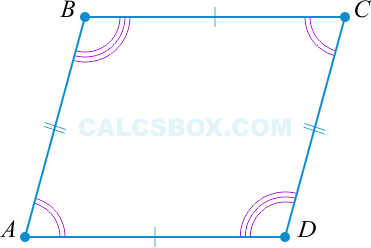
Параллелограмм
- Свойства параллелограмма
- 1. Противоположные стороны тождественны
- 2. Противоположные углы тождественны
- 3. Диагонали разделены пополам точкой пересечения
- Признаки параллелограмма
- 1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
- 2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
- 3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
- 4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Разновидностями параллелограмма (частные случаи) являются квадрат, прямоугольник и ромб.
Свойства параллелограмма
Первым делом проведем диагональ \( AC \). Получаются два треугольника: \( ABC \) и \( ADC \).
Так как \( ABCD \) — параллелограмм, то справедливо следующее:
\( AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.
\( AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.
Следовательно, \( \triangle ABC = \triangle ADC \) (по второму признаку: \( \angle 1 = \angle 2, \angle 3 = \angle 4 \) и \( AC \) — общая).
И, значит, \( \triangle ABC = \triangle ADC \), то \( AB = CD \) и \( AD = BC \).
Согласно доказательству свойства 1 мы знаем, что \( \angle 1 = \angle 2, \angle 3 = \angle 4 \). Таким образом сумма противоположных углов равна: \( \angle 1 + \angle 3 = \angle 2 + \angle 4 \). Учитывая, что \( \triangle ABC = \triangle ADC \) получаем \( \angle A = \angle C \), \( \angle B = \angle D \).
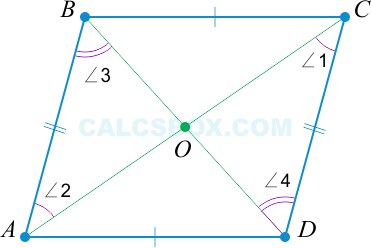
По свойству 1 мы знаем, что противоположные стороны тождественны: \( AB = CD \). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \( \triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \( BO = OD \) (напротив углов \( \angle 2 \) и \( \angle 1 \)) и \( AO = OC \) (напротив углов \( \angle 3 \) и \( \angle 4 \) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
\( AB = CD \); \( AB || CD \Rightarrow ABCD \) — параллелограмм.
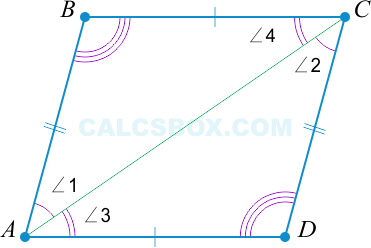
Рассмотрим подробнее. Почему \( AD || BC \)?
\( \triangle ABC = \triangle ADC \) по свойству 1: \( AB = CD \), \( \angle 1 = \angle 2 \) как накрест лежащие при параллельных \( AB \) и \( CD \) и секущей \( AC \).
Но если \( \triangle ABC = \triangle ADC \), то \( \angle 3 = \angle 4 \) (лежат напротив \( AD || BC \) (\( \angle 3 \) и \( \angle 4 \) - накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
\( AB = CD \), \( AD = BC \Rightarrow ABCD \) — параллелограмм.
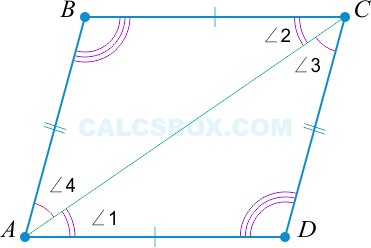
Рассмотрим данный признак. Еще раз проведем диагональ \( AC \).
По свойству 1 \( \triangle ABC = \triangle ACD \).
Из этого следует, что: \( \angle 1 = \angle 2 \Rightarrow AD || BC \) и \( \angle 3 = \angle 4 \Rightarrow AB || CD \), то есть \( ABCD \) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
\( \angle A = \angle C \), \( \angle B = \angle D \Rightarrow ABCD \) — параллелограмм.
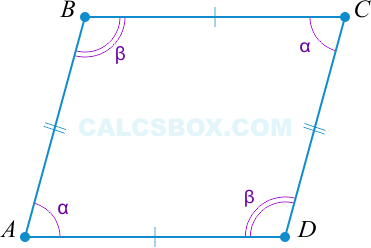
\( 2 \alpha + 2 \beta = 360^{\circ} \) (поскольку \( \angle A = \angle C \), \( \angle B = \angle D \) по условию).
Получается, \( \alpha + \beta = 180^{\circ} \). Но \( \alpha \) и \( \beta \) являются внутренними односторонними при секущей \( AB \).
И то, что \( \alpha + \beta = 180^{\circ} \) говорит и о том, что \( AD || BC \).
При этом \( \alpha \) и \( \beta \) — внутренние односторонние при секущей \( AB || CD \).
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
\( AO = OC \); \( BO = OD \Rightarrow \) параллелограмм.
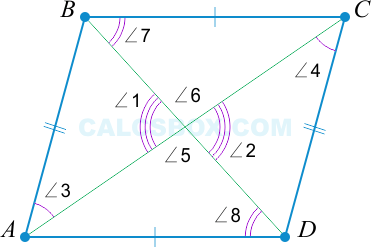
\( BO = OD \); \( AO = OC \), \( \angle 1 = \angle 2 \) как вертикальные \( \Rightarrow \triangle AOB = \triangle COD \), \( \Rightarrow \angle 3 = \angle 4 \), и \( \Rightarrow AB || CD \).
Аналогично \( BO = OD \); \( AO = OC \), \( \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 \), и \( \Rightarrow AD || BC \).
Четвертый признак верен.
