Квадрат
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба. Площадь квадрата равна квадрату его стороны. А также существует вторая формула: площадь квадрата равна половине квадрата его диагонали.
Квадрат — это четырехугольник, имеющий равные стороны и углы.
Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.
Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.
Свойства квадрата
4. Сумма всех углов квадрата равна 360 градусов
\( \angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^{\circ} \)
5. Величина угла между диагональю и стороной равна 45 градусов
\( \angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^{\circ} \)
Квадрат является ромбом \( \Rightarrow \) \( 45^{\circ} \). Тогда \( \angle A \), и \( \angle C \) на \( 45^{\circ} \).
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам
\( AO = BO = CO = DO \)
\( \angle AOB = \angle BOC = \angle COD = \angle AOD = 90^{\circ} \)
\( AC = BD \)
Так как квадрат это прямоугольник \( \Rightarrow \) диагонали равны; так как — ромб \( \Rightarrow \) диагонали перпендикулярны. А так как — параллелограмм, \( \Rightarrow \) диагонали разделены точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника
\( \triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD \)
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника
\( \triangle AOB = \triangle BOC = \triangle COD = \triangle AOD \)
9. Если сторона квадрата равна a, то, диагональ будет равна \( a \sqrt{2} \)
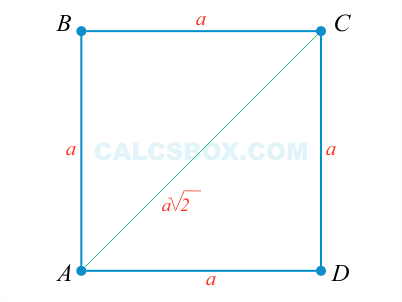
Доказывается по теореме Пифагора. Применим ее к \( \triangle ADC \).
\( AC^{2} = AD^{2} + DC^{2} = a^{2} + a^{2} = 2^{2} \)
Отсюда: \( AC = \sqrt{2}\cdot a \)
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей
